MENGGAMBAR SKETSA GRAFIK FUNGSI KUADRAT (2)
MENGGAMBAR SKETSA GRAFIK FUNGSI KUADRAT (2)
Pada
pertemuan yang lalu kita telah belajar menggambar sketsa grafik
fungsi kuadrat
Kalian bisa melihatnya lagi pada link https://rina-dewantari.blogspot.com/2020/10/menggambar-sketsa-grafik-fungsi-kuadrat.html
Pada
kesempatan kali ini kita masih membahas materi yang sama namun pada bentuk
fungsi kuadrat yang berbeda
Materi
ada di Buku Paket halaman 100-101
Sebelum melangkah ke contoh soal coba kalian ingat
kembali langkah-langkah menggambar
sketsa grafik fungsi kuadrat
1. Menentukan bentuk grafik dengan melihat nilai a
Jika a>0 artinya grafik terbuka ke atas
Jika a<0 artinya grafik terbuka ke bawah
2. Menentukan nilai Diskriminan (D)
Jika D>0 artinya grafik memotong sumbu X di dua titik
Jika D=0 artinya grafik memotong sumbu X di satu titik
Jika D<0 artinya grafik tidak memotong sumbu X
3. Menentukan titik potong terhadap sumbu X
Bisa dengan pemfaktoran maupun rumus abc (rumus kuadratik)
4. Menentukan titik potong terhadap sumbu Y
Dengan substitusi x = 0
5. Menentukan sumbu simetri
6. Menentukan nilai optimum
Merupakan gabungan dari hasil langkah 5 dan 6
8. Menggambar grafiknya pada bidang koordinat kartesius
berdasarkan hasil dari langkah 1-7
Yuk sekarang kita bersama mencoba menyelesaikan
permasalahan di bawah ini
Contoh 1
Buatlah Sketsa grafik fungsi kuadarat
f(x) = x2 – 6x + 10
Dari
fungsi diatas maka diketahui
a = 1
b = -6
c = 10
Langkah 1. Menentukan bentuk grafik
dengan melihat nilai a
Karena a > 0 maka grafik
terbuka ke atas
Langkah 2. Menentukan Nilai Diskriminan
(D)
D = b2
– 4ac
= (-6)2
– 4.1.10
= 36 –
40
= -4
Karena
D < 0 maka
grafik tidak
memotong sumbu X
Langkah 3. Menentukan titik potong
terhadap sumbu X
Nah,
karena tidak memotong sumbu X maka langkah 3 lewati
Ngapain dicari
wong tidak memiliki akar real sehingga grafiknya tidak memotong sumbu X
Hemat energi ☺
Langkah 4. Menentukan titik potong
tergadap sumbu Y
Titik
potong terhadap sumbu Y adalah jika x=0
y = x2
– 6x + 10
= 02
– 6.0 + 10
y = 10
Jadi
titik potong terhadap sumbu Y adalah ( 0,10 )
Langkah 5. Menentukan sumbu simetri
Langkah 6. Menentukan nilai optimum
Langkah 7. Menentukan koordinat titik
puncak
Koordinat
titik puncak merupakan perpaduan dari sumbu simetri dan nilai optimum pada
langkah nomor 5 dan 6
Jadi Koordinat titik puncaknya adalah (3,1)
Langkah 8. Menggambar Sketsa Grafiknya
Contoh 2
Buatlah Sketsa grafik fungsi kuadarat
f(x)=3 - 2x - x2
Wuiii… kok horror
ya bentuk fungsinya?... ☻
Tenang ambil nafas
dulu, hembuskan rileks
Yuk kita
selesaikan pelan-pelan
Ingat bentuk umum persamaan kuadrat
ax2 + bx + c = 0
Coba kamu amati, artinya :
a itu koefisien x (bilangan di depan x)
b itu koefisian y (bilangan di depan y)
c itu bilangan yang tidak bersama x atau y, yang jomblo kayak kamu
Jadi
Dari
fungsi diatas maka diketahui
a = -1
b = -2
c = 3
Langkah 1. Menentukan bentuk grafik
dengan melihat nilai a
Karena a < 0 maka
grafik terbuka ke bawah
Langkah 2. Menentukan Nilai Diskriminan
(D)
D = b2
– 4ac
= (-2)2
– 4.(-1).3
= 4 + 12
= 16
Karena
D > 0 maka
grafik memotong
sumbu X di dua titik
Langkah 3. Menentukan titik potong
terhadap sumbu X
Nah sekarang yang kita gunakan untuk menentukan titik
potong terhadap sumbu X adalah persamaan kuadrat terakhir yang sudah kita modif
Dengan
Pemfaktoran
(Cari
2 bilangan jika di tambah hasilnya -3 jika dikali hasilnya 2 yaitu 3 dan -1)
( x+3 ) ( x-1 ) = 0
x+3 =0 atau x-1=0
x1=-3 atau x2=1
Jadi
titik potong terhadap sumbu x adalah (-3,0) dan (1,0)
Langkah 4. Menentukan titik potong
tergadap sumbu Y
Untuk langkah
selanjutnya tetap gunakan fungsi awal lho ya (yang di soal)
Titik
potong terhadap sumbu Y adalah jika x=0
y = 3 - 2x - x2
= 3 –
2.0 – 02
= 3 – 0 - 0
y = 3
Jadi
titik potong terhadap sumbu Y adalah ( 0,3 )
Langkah 5. Menentukan sumbu simetri
Langkah
6. Menentukan nilai optimum
Koordinat
titik puncak merupakan perpaduan dari sumbu simetri dan nilai optimum pada
langkah nomor 5 dan 6
Jadi Koordinat titik puncaknya adalah (-1,4)
Langkah 8. Menggambar Sketsa Grafiknya
Dah… gitu aja
Gampang kan ?
Hehehe
Kalau pusing
bersyukurlah
Itu artinya kamu masih
punya kepala dan punya otak , ya kan … ?
Yuk tetap
semangat
Inilah proses
belajar
Nikmati…
Tenang Nomor Ibu
belum ganti untuk tetap membimbing kalian selalu
I Love You all
LATIHAN
Kerjakan di buku latihan kalian, kemudian
poto grafiknya
untuk dilaporkan bersama evaluasi
Diketahui
fungsi kuadrat f(x)= -x2 + 4x - 4
Tentukan
a.
Nilai a, b, dan c nya
b.
Berdasarkan
nilai a tentukan bentuk grafiknya
c.
Nilai
D
d.
Titik
potong terhadap sumbu X
(ingat trik, kalikan dengan -1 dulu)
e.
Titik
potong terhadap sumbu Y
f.
Sumbu
simetri
g.
Nilai
optimum fungsi
h.
Koordinat
titik puncak
i.
Sketsa
grafiknya

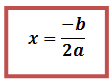










Komentar
Posting Komentar