MENGGAMBAR SKETSA GRAFIK FUNGSI KUADRAT

-

 

MENGGAMBAR GRAFIK FUNGSI KUADRAT



Pada pertemuan yang lalu kita telah belajar menggambar grafik fungsi kuadrat dengan tabel jika Daerah Asal (Domain) dari Fungsi terdebut diketahui

Kalin bisa melihatnya lagi pada link https://rina-dewantari.blogspot.com/2020/09/fungsi-kuadrat.html

Jika Domain tidak di sertakan maka tentu saja akan menemui kesulitan

Pada kesempatan kali ini kita akan mempelajari langkah-langkah menggambar sketsa grafik fungsi kuadrat tanpa harus diketahui Domainnya

Materi ada di Buku Paket halaman 99-101

Dibawah ini akan Ibu paparkan sedetail mungkin. Ibu harap kalian bisa memahami dengan baik

Siap ya

Ayo kita mulai


Sebelumnya kita kenali bagian-bagian/komponen pada grafik fungsi kuadrat




 

CONTOH

Buatlah Sketsa grafik fungsi kuadrat f(x)=x2 – 6x + 8

Dari fungsi diatas maka diketahui

a = 1

b = -6

c = 8

Langkah 1. Menentukan bentuk grafik dengan melihat nilai a

Karena a > 0 maka grafik terbuka ke atas

 

Langkah 2. Menentukan Nilai Diskriminan (D)

D = b2 – 4ac

= (-6)2 – 4.1.8

= 36 – 32

= 4

Karena D > 0 maka grafik memotong sumbu X di dua titik

 

Langkah 3. Menentukan titik potong terhadap sumbu X

x2 – 6x + 8 = 0

Dengan Pemfaktoran

(Cari 2 bilangan jika di tambah hasilnya -6 jika dikali hasilnya 8)

( x-2 ) ( x-4 ) = 0

x-2 =0 atau x-4=0

x1=2 atau x2=4

Jadi titik potong terhadap sumbu x adalah (2,0) dan (4,0)

 

Langkah 4. Menentukan titik potong terhadap sumbu Y

Titik potong terhadap sumbu Y adalah jika x=0

y = x2 – 6x + 8

   = 02 – 6.0 + 8

y = 8

Jadi titik potong terhadap sumbu Y adalah ( 0,8 )

Langkah 5. Menentukan sumbu simetri




Langkah  6. Menentukan nilai optimum


Jadi nilai optimumnya adalah y = -1




Langkah 7. Menentukan koordinat titik puncak

Koordinat titik puncak merupakan perpaduan dari sumbu simetri dan nilai optimum pada langkah nomor 5 dan 6

Jadi Koordinat titik puncaknya adalah (3,-1)

 

Langkah 8. Menggambar Sketsa Grafiknya

 


Demikian paparan materi dari Ibu. Agak panjang ya caranya. namun gampang kok


Yuk untuk menguji pemahaman kalian cobalah untuk mengerjakan latihan di bawah ini. 

Silahkan saling sharing antar teman . Ibu akan tetap memantau dan membimbing kalian melalui WAG

Selamat berlatih

SEMANGAT...


LATIHAN

Kerjakan di buku latihan kalian, kemudian poto hasilnya untuk dilaporkan bersama evaluasi

Diketahui fungsi kuadrat f(x) = x2 - 4x - 5

Tentukan :

a.    Berdasarkan nilai a tentukan bentuk grafiknya

b.    Nilai D

c.    Titik potong terhadap sumbu X

d.    Titik potong terhadap sumbu Y

e.    Sumbu simetri

f.     Nilai optimum fungsi

g.    Koordinat titik puncak

h.    Sketsa grafiknya


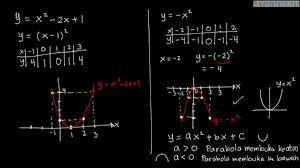
Komentar

Posting Komentar

Postingan populer dari blog ini

APLIKASI KEKONGRUENAN DAN KESEBANGUNAN DALAM KEHIDUPAN SEHARI-HARI

-
Gambar
  APLIKASI KEKONGRUENAN DAN KESEBANGUNAN DALAM KEHIDUPAN SEHARI-HARI   Dalam 4 minggu ke belakang kita telah belajar tentang konsep kesebangunan dan kekongruenan   Banyak hal-hal di kehidupan yang tanpa kamu sadari menggunakan konsep kekongruenan dan kesebangunan Diantaranya pemasangan lantai keramik, pembuatan lemari, atap, pintu dan jendela, pencetakan foto, membuat miniatur bangunan, menggambar peta dan masih banyak lagi   Dan tahukah kamu cara menghitung tinggi gunung, diameter bumi, jarak bumi ke matahari, luas galaksi itupun menggunakan konsep kesebangunan Ga mungkin kan pakai meteran ??? Meterannya sepanjang apa coba?   Nah kalian juga bisa lho mengukur tinggi pohon, tinggi tiang bendera, bahkan tinggi gedung pencakar langit, lebar sungai dll tanpa repot-repot naik pohon/tiang bendera untuk mengukurnya   Perhatikan ilustrasi di bawah ini   Kasus 1 Ahmad  ingin mengganti tali yang ada pada tiang bendera di sekolahnya. Oleh karena itu, ia perlu meng
Baca selengkapnya

BAB 10 PELUANG (2)

-
Gambar
  BAB 10 PELUANG (2) PELUANG TEORETIK Pada pertemuan yang lalu kita telah belajar tentang beberapa contoh kejadian dalam kehidupan sehari-hari yang berkaitan dengan peluang, pengertian dan istilah-istilah dalam materi peluang. Peluang terbagi dalam 2 jenis yaitu Peluang Empirik dan Peluang Teoretik. Minggu lalu kita susdah membahas Peluang Empirik Peluang empirik adalah nilai peluang yang dihitung setelah dilakukan percobaan. Materi dan contoh bisa kalian lihat lagi di https://rina-dewantari.blogspot.com/2021/05/bab-10-peluang-1.html Hari ini kit lanjutkan bahasannya dengan PELUANG TEORETIK A.       Pengertian Peluang Teoretik Peluang empirik adalah nilai peluang yang dihitung “setelah” dilakukan percobaan Nah kalau peluang teoretik adalah nilai peluang yang dihitung “sebelum” dilakukan percobaan. Peluang teoretik adalah semacam prediksi dari suatu kejadian tertentu Peluang teoretik menghitung nilai kemungkinan dari suatu kejadian yang di harapkan Misalnya d
Baca selengkapnya

BAB 10 PELUANG (1)

-
Gambar
  BAB 10 PELUANG (1) Materi bahasan kita kali ini mungkin masih asing, karena belum pernah di bahas di SD maupun kelas VII. Tapi materinya gampang banget. Walaupun kalian belum pernah mempelajarinya secara sains, namun sudah sering kalian lihat dan praktekkan dalam kehidupan sehari-hari Manfaat dari mepelajari materi ini tentu saja erat kaitannya juga untuk kehidupan kalian agar lebih terencana dalam melakukan sesuatu atau membuat sebuah keputusan. Berikut contohnya Pada saat kalian bermain ular tangga kalian menggunakan dadu. Banyak langkah pin kalian di papan ular tangga tidak boleh semaunya, tetapi di tentukan oleh banyak titik yang tertera pada dadu yang kalian lemparkan. Pin yang pertama sampai di titik akhir, itulah yang menang. Kemudian pada saat awal pertandingan sepakbola, untuk menentukan tim mana yang pertama kali melakukan kick off (tendangan pembuka) maka wasit akan mengundi dengan melempar koin yang memiliki sisi berbeda disaksikan kapten masing-masing tim. Tim
Baca selengkapnya