BAB 1 POLA BILANGAN

Memahami Macam – Macam Pola Bilangan Dalam Matematika

Macam – macam pola bilangan |

Pola bilangan merupakan sub bab dari materi barisan bilangan atau bab yang perlu di fahami terlebih dahulu sebelum melanjut pada materi barisan aritmatika dan barisan geometri.

Pola bilangan sendiri memiliki arti suatu susunan bilangan yang memiliki bentuk teratur atau suatu bilangan yang tersusun dari beberapa bilangan lain yang membentuk suatu pola . Dan pola bilangan juga memiliki banyak jenisnya atau macamnya . Pada kesempatan kali ini , kita akan mempelajarinya bersama .

Macam – macam Pola Bilangan

Macam – macam pola bilngan meliputi beberapa jenis berikut ini :

1. Pola Bilangan Ganjil 

Poal bilangan ganjil yaitu pola bilangan yang terbentuk dari bilangan – bilangan ganjil . Sedangkan pengertian dari bilangan ganjil sendiri memiliki arti suatu bilangan asli yang tidak habis dibagi dua ataupun kelipatannya .

• pola bilangan ganjil adalah :  1 , 3 , 5 , 7 , 9 , . . . .
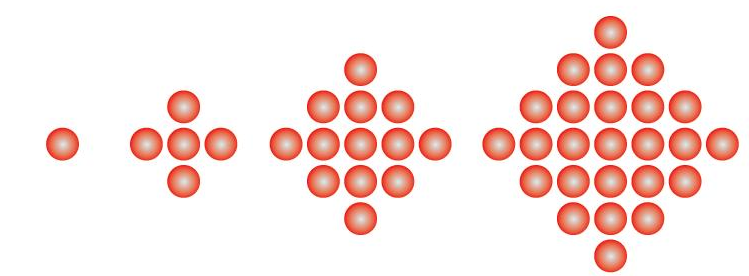
• Gambar Pola bilangan ganjil :

• Rumus Pola Bilangan ganjil

1 , 3 , 5 , 7 , . . . , n , 

(+2, +2, +2, +2, ... )

maka rumus pola bilangan ganjil ke n adalah :

Un = 2n – 1 

Contoh :

1 , 3 , 5 , 7 , . . . , ke 10

Berapakah pola bilangan ganjil ke 10 ?

Jawab :

Un = 2n – 1

U10 = 2 . 10 – 1

        = 20 – 1   = 19

2. Pola Bilangan Genap 

pola bilangan genap yaitu pola bilangan yang terbentuk dari bilangan – bilangan genap . Bilangan genap yaitu bilangan asli yaitu bilangan asli yang habis dibagi dua atau kelipatannya .

• Pola bilangan genap adalah : 2 , 4 , 6 , 8 , . . .
• Gambar pola bilangan genap :

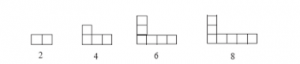
• Rumus Pola bilangan genap

2 , 4 , 6 , 8 , . . . . , n  

Pola (+2, +2, +2, ...)

maka rumus pola bilangan genap ke n adalah : 

Un = 2n 

Contoh :

2 , 4 , 6 , 8 , . . . ke 10 .berapakah pola bilangan genap ke 10 ?

jawab :

Un = 2n

U10 = 2 x 10

        = 20

3. Pola bilangan Persegi 

Pola bilangan persegi , yaitu suatu barisan bilangan yang membentuk suatu pola persegi .

• Pola bilangan persegi adalah 1 , 4 , 9 , 16 , 25 ,  . . .

         Pola (+3, +5, +7, +9, ...)

• Gambar Pola bilangan persegi :

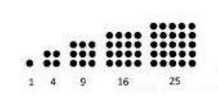
• Rumus Pola bilangan persegi

1 , 4 , 9 , 16 , 25 , 36 , . . . , n  maka rumus untuk mencari pola bilangan persegi ke n adalah :

Un =  n²

Contoh :

Dari suatu barisan bilangan 1 , 2 , 9 , 16 , 25 , 36 , . . . ,ke 10 . Berapakah pola bilangan ke 10 dalam pola bilangan persegi ?

Jawab :

Un = n²

U10 = 10²     = 100

4. Pola Bilangan Persegi Panjang 

Pola bilangan persegi panjang yaitu suatu barisan bilangan yang membentuk pola persegi panjang .

• Pola persegi panjang adalah 2 , 6 , 12 , 20 , 30 , . . .
• Gambar Pola Bilangan persegi panjang :

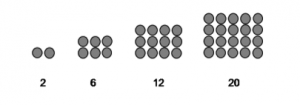
• Rumus pola bilangan persegi panjang

2 , 6 , 12 , 20 , 30 , . . .  n  , 

Pola (+4, +6, +8, +10, ...)

maka Rumus Pola bilangan Persegi panjang ke n adalah :

Un = n . n + 1 

Contoh :

Dari suatu barisan bilangan 2 , 6 , 12 , 20 , 30 , . . . , ke 10 . Berapakah pola bilangan persegi ke 10 ?

Jawab :

Un = n . n+ 1

U10 = 10 . 10 + 1

        = 10 . 11

       = 110

5. Pola Bilangan Segitiga 

Pola bilangan segitiga yaitu suatu barisan bilangan yang membentuk sebuah pola bilangan segitiga .

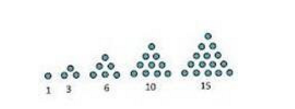
• Pola bilangan segitiga adalah : 1 , 3 , 6 , 10 , 15 , . . .
• Gambar Pola bilangan segitiga :

• Rumus Pola Bilangan Segitiga :

1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke n . 

Pola (+2, +3, +4, +5 ....)

Maka rumus pola bilangan segitiga ke n adalah : 

Un = 1 / 2 n ( n + 1 ) 

Contoh Soal :

Dari suatu barisan bilangan 1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke 10 . Berapakah pola bilangan segitiga ke 10 ?

Jawab :

Un = 1/2 n ( n + 1 )

U 10 = 1/2 .10 ( 10 + 1 )

         = 5 ( 11 )  = 55

6. Pola Bilangan FIBONACCI 

Pola bilangan fibonacci yaitu suatu bilangan yang setiap sukunya merupakan jumlah dari dua suku di depanya .

• Pola bilangan fibonacci :

1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 56 , . . .

2 , 2 , 4 , 6 , 10 , 16 , 26 , 42 , . . ..

Pola = Suku ke 3 dan seterusnya merupakan hasil penjumlahan dari 2 suku sebelumnya

7. Pola Bilangan Pascal

Apa itu bilangan pascal? Sebenarnya bilangan ini ditemukan oleh seorang penemu Prancis yang bernama Blaise Pascal. Oleh karena itu namanya jadi bilangan pascal karena diambil dari namanya, yaitu Pascal. Bilangan ini terbentuk dari sebuah aturan geometri yang berisi susunan koefisien binomial yang bentuknya menyerupai segitiga. Di dalam segitiga pascal, bilangan yang terdapat pada satu baris yang sama dijumlahkan menghasilkan bilangan yang ada di baris bawahnya. 

Itulah tadi sekilas penjelasan mengenai bilangan pascal itu sendiri, ya. Sekarang kita bahas pola bilangan pascalnya. Jadi, Pola bilangan pascal adalah suatu pola yang tersusun dari beberapa angka berdasarkan rumus:

 

Segitiga Pascal (sumber: MathLibraryRukmantara.com)

Berdasar gambar diatas, pola bilangan pascalnya yaitu jumlah seluruh bilangan yang ada pada baris yang sama. Coba lihat baris terakhir (baris ke 5) pada segitiga pascal di atas. Setelah dijumlahkan hasilnya 16. 16 inilah yang merupakan suku bilangan ke 5 (karena terdapat pada baris ke-5) dari pola bilangan pascal. Atau kamu juga dapat langsung menggunakan rumusnya, yaitu 2^n-1. Misalnya kamu ingin mencari suku ke 10, kamu bisa langsung masukkan ke dalam rumusnya saja. Jadi, 2^10-1 = 2⁹ = 512. Berikut pola bilangan pascal: 1, 2, 4, 8, 16, 32, 64, ... Seperti itu ya 

Agar lebih jelas kalian bisa tonton video dengan klik link berikut...

https://www.youtube.com/watch?v=eiH_ISaX3RE

Demikian penjelasan mengenai pola bilangan dalam ilmu matematika . Pada dasarnya , pola bilangan merupakan suatu bentuk barisan bilangan . Apabila kita dalam memperhatikanya tidak terlalu cermat, maka pola yang satu dengan pola bilangan yang lain tidak ada bedanya . Namun , pola bilangan memiliki fungsi yang sangat besar yaitu supaya lebih mudah dalam mengerjakan barisan aritmatika dan geometri . Semoga bermanfaat . . .

Setelah kalin mencermati materi diatas coba tes pemahaman kalian dengan mencoba latihan dibawah ini

Kerjakan di buku latihan kalian

Tentukan 3 bilangan selanjutnya dari pola bilangan berikut ini !

1. 1, 3, 5, 7, 9, ..., ..., ...

2. 5, 10, 15, 20, ..., ..., ...

3. 100, 95, 90, 85, ..., ..., ...

4. 2, 4, 8, 16, 32, ..., ..., ...

5. 800, 400, 200, ..., ..., ...

6. 2, 4, 8, 14, 22, ..., ..., ...

7. 1, 4, 9, 16, ..., ..., ...

8. 1, 3, 4, 7, 11, ..., ..., ...

Sebagai Assesment/ penilaian silahkan klik link berikut

http://gg.gg/mat-8-pola-bilangan-1

Selamat mengerjakan, semoga sukses

SEMANGAT ...